树形结构

树

树是一个类似于链表的二维结构，每个节点可以指向 0 个或多个其他节点

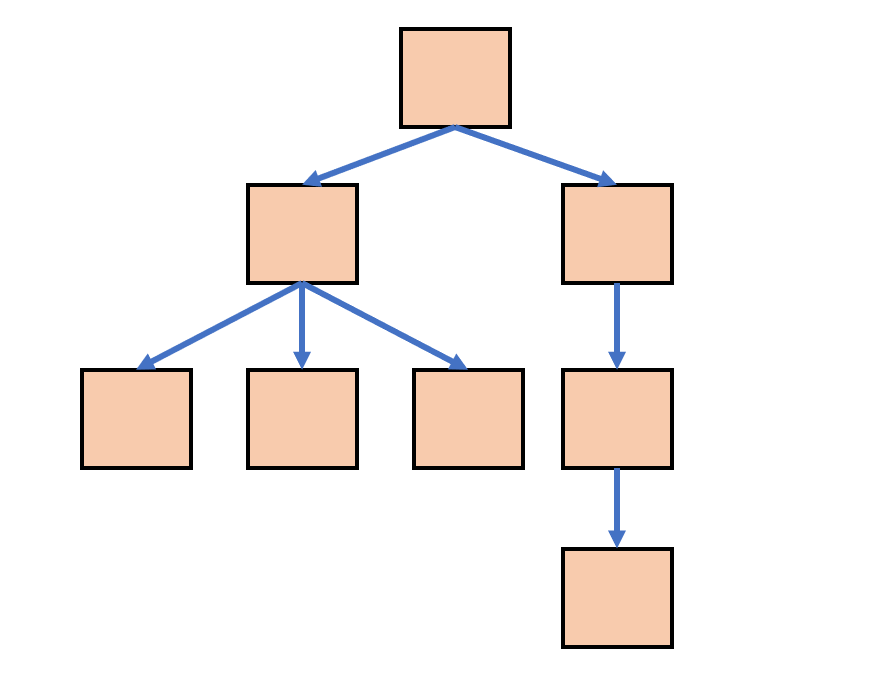
树具有以下特点：

单根：如果一个节点 A 指向了另一个节点 B，仅能通过 A 直接找到 B 节点，不可能通过其他节点直接找到 B 节点
无环：节点的指向不能形成环

树的术语：

结点的度：某个节点的度 = 该节点子节点的数量
树的度：一棵树中，最大的节点的度为该树的度
结点的层：从根开始定义起，根为第 1 层，根的子结点为第 2 层，以此类推；
树的高度或深度：树中结点的最大层次
叶子节点：度为 0 的结点称为叶结点；
分支节点：非叶子节点
子节点、父节点：相对概念，如果 A 节点有一个子节点 B，则 A 是 B 的父节点，B 是 A 的子节点
兄弟节点：如果两个节点有同一个父节点，则它们互为兄弟节点
祖先节点：某个节点的祖先节点，是从树的根到该节点本身经过的所有节点
后代节点：如果 A 是 B 的祖先节点，B 则是 A 的后代节点

树的代码表示法：

function Node(value) {
 this.value = value
 this.children = []
}

二叉树

如果一颗树的度为 2，则该树是二叉树

二叉树可以用下面的代码表示

function Node(value) {
 this.value = value
 this.left = null
 this.right = null
}

二叉树的相关算法

编写各种函数，实现下面的功能

对二叉树遍历打印

前(先)序遍历 DLR

/**
 * 前序遍历
 * @param {*} root
 */
function DLR(root) {
 //输出自己
 if (!root) {
  return
 }
 console.log(root.value)
 //输出左边
 DLR(root.left)
 //输出右边
 DLR(root.right)
}

中序遍历 LDR

/**
 * 中序遍历
 * @param {*} root
 */
function LDR(root) {
 if (!root) {
  return
 }
 //输出左边
 LDR(root.left)
 //输出自己
 console.log(root.value)
 //输出右边
 LDR(root.right)
}

后序遍历 LRD

/**
 * 后续遍历
 * @param {*} root
 */
function LRD(root) {
 if (!root) {
  return
 }
 // 输出左边
 LRD(root.left)
 // 输出右边
 LRD(root.right)
 // 输出自己
 console.log(root.value)
}

根据前序遍历和中序遍历结果，得到一颗二叉树

/**
 * 根据前序遍历和中序遍历的结果，得到一颗二叉树
 * @param {Array} dlr 数组
 * @param {Array} ldr 数组
 */
function getTree(dlr, ldr) {
 //严谨性判断
 if (dlr.length !== ldr.length) {
  throw new Error('无解')
 }
 if (dlr.length === 0) {
  return null
 }
 // 正常逻辑
 var rootValue = dlr[0] //前序遍历的第一个就是根，得到根的值
 var root = new Node(rootValue) //创建根节点

 //加左节点
 var index = ldr.indexOf(rootValue) //根节点在中序遍历中的索引
 var leftLDR = ldr.slice(0, index) //左边的中序遍历结果
 var leftDLR = dlr.slice(1, 1 + leftLDR.length) //左边的前序遍历结果
 root.left = getTree(leftDLR, leftLDR)

 //加右节点
 var rightLDR = ldr.slice(index + 1) //右边的中序遍历结果
 var rightDLR = dlr.slice(1 + leftLDR.length)

 root.right = getTree(rightDLR, rightLDR)

 return root
}

计算树的深度

/**
 * 得到树的深度
 * @param {*} root
 */
function getDepth(root) {
 if (!root) {
  return 0
 }
 return 1 + Math.max(getDepth(root.left), getDepth(root.right))
}

查询二叉树

深度优先 Depth First Search

/**
 * 深度优先搜索
 * 搜索target在树中是否存在
 * @param {*} root
 * @param {*} target
 */
function searchDeep(root, target) {
 if (!root) {
  return false
 }
 console.log(root.value)
 //先看自己
 if (root.value === target) {
  return true //找到了
 }
 // 左边或右边任何一个找到，都行
 return searchDeep(root.left, target) || searchDeep(root.right, target)
}

广度优先 Breadth First Search

/**
 * 广度优先搜索
 * 搜索target在树中是否存在
 * @param {*} root
 * @param {*} target
 */
function searchWide(root, target) {
 if (!root) {
  return false
 }
 /**
  * 辅助函数
  * @param {*} layer 要搜索的节点数组
  */
 function _searchWide(layer) {
  if (layer.length === 0) {
   return false //这一层没有东西了
  }
  console.log(layer)
  var nextLayer = [] //下一层的数组
  for (var i = 0; i < layer.length; i++) {
   if (layer[i].value === target) {
    return true
   } else {
    if (layer[i].left) {
     nextLayer.push(layer[i].left)
    }
    if (layer[i].right) {
     nextLayer.push(layer[i].right)
    }
   }
  }

  //说明这一层没有希望
  return _searchWide(nextLayer)
 }
 return _searchWide([root])
}

比较两棵二叉树，得到比较的结果

/**
 * 得到两颗树的差异
 * [
 *    {type: "修改", from: B, to: T},
 *    {type: "删除", from: D, to: null},
 *    {type: "新增", from: null, to: F},
 * ]
 * @param {*} root1
 * @param {*} root2
 */
function diff(root1, root2) {
 var result = [] //保存差异结果的数组
 if (!root1 && !root2) {
  //两棵树都没有节点
  return result
 }
 if (!root1 && root2) {
  //左边没有，右边有
  result.push({
   type: '新增',
   from: root1,
   to: root2
  })
 } else if (root1 && !root2) {
  //左边有，右边没有
  result.push({
   type: '删除',
   from: root1,
   to: root2
  })
 } else if (root1.value !== root2.value) {
  //两边的值不一样
  result.push({
   type: '修改',
   from: root1,
   to: root2
  })
  //比较后续
  var resultLeft = diff(root1.left, root2.left) //左边的差异
  var resultRight = diff(root1.right, root2.right) //右边差异
  result = result.concat(resultLeft)
  result = result.concat(resultRight)
 } else {
  //两边一样
  //比较后续
  var resultLeft = diff(root1.left, root2.left) //左边的差异
  var resultRight = diff(root1.right, root2.right) //右边差异
  result = result.concat(resultLeft)
  result = result.concat(resultRight)
 }

 return result
}

# 树形结构

# 树

# 二叉树

# 二叉树的相关算法

树形结构

树

二叉树

二叉树的相关算法