图结构

概念

图结构

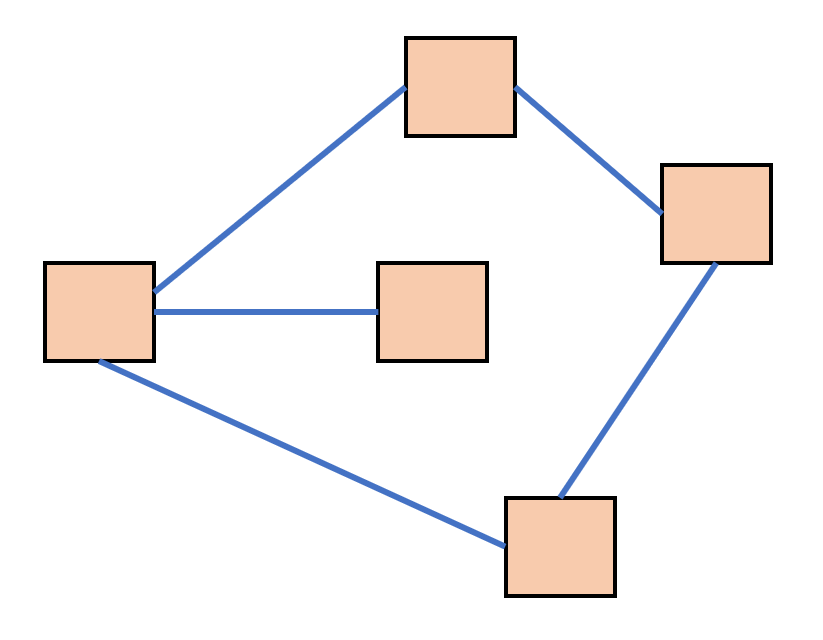
图结构中，一个结点可以链接到任意结点，所有结点链接而成的结构，即为图结构

图结构中的链接可以是有向的，也可以是无向的（双向链接），本文仅讨论双向链接

树结构是一种特殊的图结构

图结构没有根，可以有环，但是在一个图结构中，不能存在两个或以上的孤立结点

可以使用图中任何一个结点表示整个图结构

图结构是一种常见的数据结构，例如网络爬虫抓取的网页就是一种典型的图结构

图结构的代码可表示为：

function Node(value) {
 this.value = value
 this.neighbors = []
}

相关算法

查询算法

和树结构一样，图结构的查询也可以分为深度优先（Depth First Search）和广度优先(Breadth First Search)查询
Js 代码:

// 查询某个值在图中是否存在
/**
 * 深度优先搜索
 * @param {*} node
 * @param {*} targetValue
 */
function searchDeep(node, targetValue) {
 if (!node) {
  return false
 }
 var finded = [] //保存已经找过的节点
 //检查当前节点，以及节点的邻居是否满足要求
 //表示：自己和邻居有没有
 function _search(node) {
  // console.log(finded.map(it => it.value), node.value);
  // finded.includes() 判断指定的值是否在数组中存在
  if (finded.includes(node)) {
   return false //没有找到
  }
  // 该节点没有验证过
  if (node.value === targetValue) {
   return true
  }
  finded.push(node) //加入到已查找的节点中
  for (var i = 0; i < node.neighbors.length; i++) {
   var nodeNeighbor = node.neighbors[i] //拿到邻居节点
   if (_search(nodeNeighbor)) {
    return true
   }
  }
  return false
 }
 return _search(node)
}

/**
 * 广度优先搜索
 * @param {*} node
 * @param {*} targetValue
 */
function searchWide(node, targetValue) {
 if (!node) {
  return false
 }
 var finded = [] //已找过的节点

 /**
  * 查找这一群节点中是否有要找的值
  * @param {*} nodes 数组
  */
 function _search(nodes) {
  console.log(nodes)
  if (nodes.length === 0) {
   return false //没有东西了
  }
  var nexts = [] //我接下来要找的范围
  // 遍历nodes，看每一个是不是，如果不是，把它邻居加入到一个新数组中
  for (var i = 0; i < nodes.length; i++) {
   var n = nodes[i]
   if (n.value === targetValue) {
    //找到了
    return true
   }
   finded.push(n) //加入到找过的节点中
   //这个节点不是，把它的邻居加入到一个数组中
   for (var j = 0; j < n.neighbors.length; j++) {
    if (!nexts.includes(n.neighbors[j])) {
     nexts.push(n.neighbors[j])
    }
   }
  }
  // 把已经找过的从下一层中删除
  for (var i = 0; i < nexts.length; i++) {
   if (finded.includes(nexts[i])) {
    //已经找过了
    nexts.splice(i, 1)
    i--
   }
  }
  //准备找下一层
  return _search(nexts)
 }

 return _search([node])
}

最小生成树算法

如果一个图中结点连接而成的边具备某种数值，需要将这些边进行精简，生成一个连接全节点同时总边长最小的树结构，该树称之为最小生成树
实现最小生成树可以使用 Prim 算法，从任意一个点出发，连接到该点最短的点，组成一个部落，然后继续连接到该部落最短的点，直到把所有点连接完成
Js 代码：

function Prim(nodes, sides) {
 if (nodes.length <= 1 || nodes.length !== sides.length) {
  return //抱歉，臣妾做不到
 }
 var hords = [nodes[0]] //把第一个点组成一个部落
 while (hords.length < nodes.length) {
  // 向部落中增加一个点
  _addNodeToHords()
  console.log(hords.map((it) => it.value))
 }

 /**
  * 添加一个点到部落
  */
 function _addNodeToHords() {
  //1. 从nodes中选出一个到部落最近的点
  var result = _chooseNearNodeToHord()
  //2. 将该点和部落中的某个点连接起来
  result.node.neighbors.push(result.target)
  result.target.neighbors.push(result.node)
  //3. 加入到部落中
  hords.push(result.node)
 }

 /**
  * 选一个距离当前部落最近的点
  * 返回：
  * {
  *    node: 到部落最近的点,
  *    target: 连接到部落的哪个点
  * }
  */
 function _chooseNearNodeToHord() {
  var result = {
   node: null,
   target: null,
   dis: Infinity
  }
  for (var i = 0; i < nodes.length; i++) {
   //一个点一个点拿出来，看哪个点离部落最近
   var n = nodes[i]
   if (hords.includes(n)) {
    //部落里面已经有这个点了
    continue //这个点不用看了，下一个点
   }
   // 得到 n 到 部落最近的那个点的距离
   // { dis: 到部落的最短距离,  target: 到部落的点}
   var temp = _getMinDisToHord(n)
   if (temp.dis < result.dis) {
    result.node = n
    result.target = temp.target
    result.dis = temp.dis
   }
  }
  return result
 }

 /**
  * 得到指定的点到部落的最短距离，以及目标点
  * { dis: 到部落的最短距离,  target: 到部落的点}
  * @param {*} node
  */
 function _getMinDisToHord(node) {
  var result = {
   target: hords[0],
   dis: Infinity
  }
  //循环部落
  for (var i = 0; i < hords.length; i++) {
   var target = hords[i] //拿到部落的当前点
   //计算 node 到 target 的距离
   var row = nodes.indexOf(node)
   var col = nodes.indexOf(target)
   var dis = sides[row][col]
   if (dis < result.dis) {
    result.target = target
    result.dis = dis
   }
  }
  return result
 }
}

//一群孤立的节点
var a = new Node('a')
var b = new Node('b')
var c = new Node('c')
var d = new Node('d')
var e = new Node('e')

var nodes = [a, b, c, d, e]
var sides = [
 [0, 7, 9, 6, Infinity], // a到其他点的距离
 [7, 0, Infinity, 8, 4], // b到其他点的距离
 [9, Infinity, 0, Infinity, Infinity], // c到其他点的距离
 [6, 8, Infinity, 0, Infinity], // d到其他点的距离
 [Infinity, 4, 5, Infinity, 0] // e到其他点的距离
]

Prim(nodes, sides)

# 图结构

# 概念

# 相关算法

图结构

概念

相关算法